Leetcode - 52. N皇后 II 回溯算法求解

N皇后问题 - leetcode

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。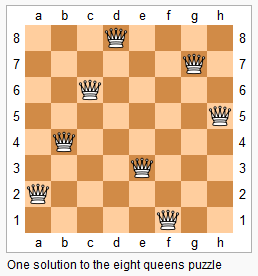
上图为 8 皇后问题的一种解法。给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例：

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。

[
[".Q..",  // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.",  // 解法 2
"Q...",
"...Q",
".Q.."]
]

解题思路：

使用回溯算法，深度优先搜索，进行遍历查询深度优先搜索的条件是有能够判断棋盘是否能落子的依据。

我这边使用一个长度为N的数组存储第J列是否有棋子，使用两个N*2-1长度的数组分别存储左对角线和右对角线是否有棋子。

对于左右对角线来说，左对角线的每一个位置i与j的和都相同，右对角线的每一个位置的i与j的差都相同，所以可以用来判断某个位置的斜线上是否存在棋子，对应对角线的数组标志为有或者没有。

代码如下

public class Solution {
  /** 总记录数 */
  private int total = 0;
  /** N皇后 */
  private int N;
  /** 判断当前位置的左对角线是否存放了棋子 */
  private int[] left = new int[15];
  /** 判断当前位置的右对角线是否存放了棋子 */
  private int[] right = new int[15];
  /** 判断当前位置的列是否存放了棋子 */
  private int[] curn;

  public int totalNQueens(int n) {
    this.N = n;
    curn = new int[n];
    left = new int[2 * n - 1];
    right = new int[2 * n - 1];
    calResult(0);
    return total;
  }

  private void calResult(int i) {
    // 棋盘第i行 遍历判断第j列
    for (int j = 0; j < N; j++) {
      // 开始判断第i行第j列
      // 判断第j列是否已经有棋子；判断(i,j)的左对角线是否有棋子；判断右对角线是否有棋子
      if (curn[j] == 0 && left[i + j] == 0 && right[N - 1 + i - j] == 0) {
        // 没有棋子 就可以在(i,j)放置棋子
        curn[j] = left[i + j] = right[N - 1 + i - j] = 1;
        // 如果N行都放置了棋子 total就加1 否则继续放置下一行
        if (i < N - 1) {
          calResult(i + 1);
        } else {
          total++;
        }
        // 放置完成之后 (i,j)位置棋子去掉，然后重新走下一步 进行深度优先搜索
        curn[j] = left[i + j] = right[N - 1 + i - j] = 0;
      }
    }
  }

  public static void main(String[] args) {
    final Solution solution = new Solution();
    solution.totalNQueens(8);
    System.out.println("total = " + solution.total);
  }
}