什么是二叉树?
在数据结构中,对于树,每一个分支,称之为一个度。那么,度最大为2的树我们称之为二叉树。通常子树我们会称之为左子树和右子树。二叉树通常用于实现二叉查找树和二叉堆。那么在Java中如何定义一个二叉树节点?
首先,每一个节点需要有一个值域。其次,其还应该持有两个树节点的引用,即指向自己的左子树和自己的右子树。
具体代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
this.val = 0;
this.left = null;
this.right = null;
}
TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
public String toString() {
return "(" + val + ")[left:" + left + ",right:" + right + "]";
}
}
如何创建二叉树
二叉树的节点的数据结构已经用Java代码表示出来了,那么如何用这些节点来构造出一个完整的二叉树呢?请看下图二叉树的结构:
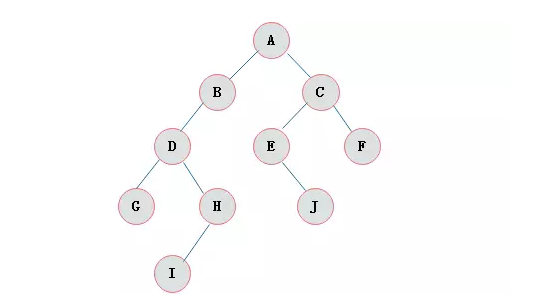
如上图,对于一个二叉树,需要有一个根节点。每个节点最多有两课子树,分别区分左子树还是右子树。即就算有一个子树,还是需要区分是左子树还是右子树。创建二叉树我们只需要将每一个树节点按照这样的规则连接起来即可。
创建二叉搜索树
- 概念:二叉搜索树,又叫二叉查找树。他是一棵特殊的二叉树,对于二叉搜索树中的每一个节点,它的左子树都不大于父节点,右子树都不小于父节点。空树是特殊的二叉搜索树。
创建:本例根据一个已有的数组进行二叉树的创建,基本的思路就是遍历数组,每个元素创建一个树节点,然后继续根据节点值得大小向下遍历判断,最后将值域小的放在节点的左子树,将值大的放在节点的右子树即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25public static TreeNode createSearchTree(int[] a) {
if (a.length > 0) {
TreeNode root = new TreeNode(a[0]);
for (int i = 1; i < a.length; i++) {
TreeNode c = root;
TreeNode p = c;
TreeNode q = new TreeNode(a[i]);
while (c != null) {
p = c;
if (a[i] <= c.val) {
c = c.left;
} else {
c = c.right;
}
}
if (q.val < p.val) {
p.left = q;
} else {
p.right = q;
}
}
return root;
}
return null;
}特点:二叉搜索树在应用于经常查找元素的场景效率会比较快,因为它的数据结构类似于二分查找,查找元素时根据其特性向下搜索即可。
创建完全二叉树
概念:首先介绍一下满二叉树:即树中的所有节点除了叶节点都有左子树和右子树,叶节点的左右子树都为空,这样的树称之为满二叉树。而对于一棵完全二叉树,只有树的最后一层连续缺失右边节点。满二叉树一定是完全二叉树,反之则不一定成立。如图分别是一棵满二叉树和一棵完全二叉树:
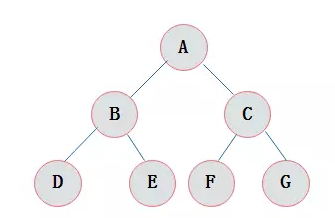
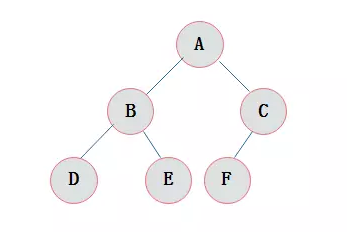
创建: 完全二叉树的创建需要按层去创建。这边我们借助队列的特点,将二叉树的节点连接起来,构造成完全二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public static TreeNode createWholeTree(int[] a) {
if (a.length > 0) {
LinkedList<TreeNode> queue = new LinkedList<>();
TreeNode root = new TreeNode(a[0]);
queue.add(root);
int index = 0;
for (int i = 1; i < a.length; i++) {
TreeNode curn = queue.get(index);
TreeNode ti = new TreeNode(a[i]);
queue.add(ti);
if (curn.left == null) {
curn.left = ti;
} else if (curn.right == null) {
curn.right = ti;
index++;
}
}
return root;
}
return null;
}特点:对于一个h层的完全二叉树,前h-1层是满的,第h层连续缺失右边节点。所以叶子结点只能出现在最下层和次下层,最下层的叶子结点集中在树的左部,倒数第二层若存在叶子结点,一定在右部连续位置,如果结点度为1,则该结点只有左孩子,即没有右子树,同样结点数目的二叉树,完全二叉树深度最小。
二叉树的遍历
前中后序递归遍历:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32/**
* 递归先序遍历二叉树 左-根-右
*/
public static void frontPrintOutTree(TreeNode root) {
if (null != root) {
System.out.print(root.val);
frontPrintOutTree(root.left);
frontPrintOutTree(root.right);
}
}
/**
* 递归中序遍历二叉树 左-根-右
*/
public static void midPrintOutTree(TreeNode root) {
if (null != root) {
midPrintOutTree(root.left);
System.out.print(root.val);
midPrintOutTree(root.right);
}
}
/**
* 递归先序遍历二叉树 左-根-右
*/
public static void lastPrintOutTree(TreeNode root) {
if (null != root) {
lastPrintOutTree(root.left);
lastPrintOutTree(root.right);
System.out.print(root.val);
}
}按层遍历:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21/**
* 按层遍历二叉树
*/
public static void levelPrintOutTree(TreeNode root) {
if (null != root) {
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
TreeNode i = root;
while (!queue.isEmpty()) {
if (i.left != null) {
queue.add(i.left);
}
if (i.right != null) {
queue.add(i.right);
}
System.out.print(i.val);
queue.poll();
i = queue.peek();
}
}
}

